Algorithmen zur Wegfindung
"Quo vadis?" (Historischer Monumentalfilm, übersetzt: Wohin gehst du?)
Prolog
Nicht nur in Strategie- und Rollenspielen müssen sich die vom Spieler gesteuerten Figuren von einer Position X zu einer Position Y bewegen. In immer mehr modernen Spielen wird diese Untergruppe der Algorithmen, die normalerweise mit Künstlicher Intelligenz bezeichnet wird, immer bedeutender. Interessanterweise sind die meisten Algorithmen, die sich mit der Wegsuche befassen, schon relativ alt.
Hier sollen ein paar exemplarisch dargestellt werden. Dazu wird natürlich erst einmal ein Spielfeld benötigt, hier als zweidimensionales Byte-Array World dargestellt. Die Ausweitung dieses Arrays wird über die Konstanten WORLDX und WORLDY eingestellt.
Frei wie ein Vogel - Die gerade Luftlinie
Der einfachste Weg von X nach Y zu gelangen ist die Luftlinie. Ein Vogel muss sich keine Gedanken darüber machen, welche Hindernisse sich ihm in den Weg stellen, er fliegt einfach darüber hinweg. Also ist die kürzeste Verbindung in unserer Welt die Gerade (ja, ja, Einstein sagt, die kürzeste Verbindung sei eine Gekrümmte, aber das gilt doch nur im vierdimensionalen Raum-Zeit-Kontinuum).
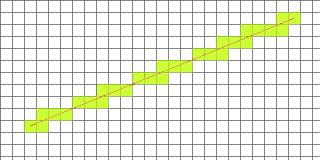
Wie zieht man eine Gerade, wenn man nur einen Start- und einen Zielpunkt hat?
Man benutzt ein Lineal, legt einen Stift an und zeichnet drauf los. Sehr schön,
geht aber nur in einem analogen Umfeld. Auf dem PC ist die Welt leider etwas
kantiger, pixeliger. Wir müssen also die jeweilige analoge Linie irgendwie
"digitalisieren", rastern.
Schauen wir uns einmal die Formel für Geraden an:
Y = mx + b
Vernachlässigen wir für den Moment den y-Achsenabschnitt b. Durch Umstellung erhalten wir die Steigung m = y/x. Da unsere Linie durch Anfangs- (x1, y1) und Endpunkt (x2, y2) festgelegt wird, errechnet sich die Steigung als
m = (y2-y1) / (x2–x1).
Addiert man jetzt in einer Schleife von x1 bis x2 immer wieder die Steigung m zu y1 und rundet diesen Wert, ergeben sich die korrekten Punktkoordinaten der Linie.
Dieses Verfahren hat leider einen entscheidenden Nachteil: Es arbeitet mit Gleitkommazahlen und rundet diese. Dadurch wird es sehr langsam. Zwar kann man die Rundung noch durch Einführung einer Variablen error ausschalten, indem innerhalb der Schleife m zu error addiert wird und error mit 0,5 verglichen wird. Dennoch bleiben die langsamen Gleitkommaoperationen.
Ein Spiel, in dem 352 Gegner auf den Spieler in gerade Linie aus verschiedenen Richtungen zustürmen, würde wahrscheinlich mehr zum Kaffeetrinken als zu irgend etwas anderem animieren. Also brauchen wir einen schnelleren Algorithmus. Und - oh, Wunder! - den gibt es sogar schon!
Bresenham-Algorithmus
[siehe z.B. J. Bresenham, Algorithm für Computer Control of a Digital Plotter. IBM Systems Journal, 4(1): 25-30, 1965]
Bresenham verzichtet bei seinem Algorithmus vollständig auf Gleitkomma-Arithmetik. Stattdessen benutzt er einen Variable, die bei Erreichen eines bestimmten Schwellwertes eine Veränderung der zu zeichnenden Koordinate bewirkt.
Betrachten wir einmal eine Gerade mit einer Steigung zwischen 0 und 1 (Alle anderen Steigungen können durch Spiegelung auf diese zurückgeführt werden, siehe weiter unten). In einer Schleife von der x-Koordinate des Startpunktes bis zur x-Koordinate des Zielpunktes wird die zugehörige y-Koordinate immer dann verändert, wenn eine Variable error, die vor der Schleife mit einem bestimmten negativen Wert initialisiert und in der Schleife immer wieder mit dy (Differenz zwischen y-Koordinate des Startpunktes und y-Koordinate des Zielpunktes) addiert wurde, wenn also eben diese Variable error 0 übersteigt.
Verdeutlichen wir das einmal an einem Beispiel:
Sei der Startpunkt gegeben durch x1 = y1 = 0 und der Zielpunkt gegeben durch x2=5 und y2 = 3. Wir erhalten dx = x2 - x1 = 5 und dy = y2 - y1 = 3. Anders ausgedrückt: Die Gerade hat eine Steigung m = 3/5. Da wir jedoch auf (langsame!) Fließkommaoperationen verzichten wollen, skalieren/muliplizieren wir die Steigung 3/5 einfach mit dx: 3/5 * 5 = 3.
Dazu benutzen wir die Variable error und initialisieren diese mit dem ganzzahligen Wert -dx/2 (Diese Operation läßt sich übrigens schnell durch eine bitweise Rechtsverschiebung, ein SHR oder ShiftRight, erzielen). Die Inititalisierung mit dem hälftigen dx begründet sich übrigens in dem bereits oben dargestellten Vergleich mit 0,5 der error – Variablen in der Gleitkomma-Variante.
Durch diese Skalierung werden in der Schleife nur noch ganzzahlige Werte verglichen, die langsamen Gleitkomma-Operationen sind eliminiert.
Wie oben bereits erwähnt kann man Geraden mit anderen Steigungen durch Spiegelung erzielen. Bei einer Gerade mit einer negativen Steigung zwischen 0 und –1 ersetzt man einfach das zu setzende y durch –y, sofern der Zielpunkt rechts vom Startpunkt liegt. Liegt er links vom Startpunkt wird x durch –x ersetzt.
Allgemein für beliebige Steigungen lautet der Bresenham-Algorithmus wie folgt:
[siehe C++ - Programm, Routine: Airline)
Step by step! Aber
nur den besten...
"Es kann nur einen geben!" (Highlander)
Soviel zu Vögeln, Bulldozern, Dinosauriern und anderen Subjekten, die sich nicht um Wegkosten kümmern müssen. Ab jetzt kommen aber eben diese Wegkosten ins Spiel. Was sind Wegkosten aber überhaupt?
Bewegung kostet Kraft. Ein Schritt von einem Weltfeld zu einem gleichhohen Nachbarn kostet (per definitionem) einen Bewegungspunkt. Ist das Nachbarfeld aber eine Stufe höher (oder niedriger), benötigt die Spielfigur einen weiteren Bewegungspunkt, um diesen Höhenunterschied zu überwinden. Vereinfachend nehmen wir folgende Gleichung an:
Bewegungpunkte = 1 + abs(Höhe Nachbarfeld - Höhe AktuellesFeld)
(Anmerkung: Sinnvoller wäre evt. eine Funktion, die größere Höhenunterschiede mit mehr Bewegungspunkten "bestraft".)
Der Algorithmus BestNextStep wählt nun einfach von den in Zielrichtung liegenden Nachbarpunkten denjenigen aus, der die geringsten Wegekosten aufweist. Im Beispielprogramm beschränken wir uns auf die vier Richtungen links, rechts, oben und unten, so dass lediglich das Minimum von maximal zwei Werten gefunden werden muss.
Dieser Algorithmus findet zwar relativ schnell seinen Weg, versagt aber bei größeren Hindernissen im Weg. Somit ist er in der reinen Form eher unbrauchbar, aber als (beschleunigender) Teil einer Dijkstra- oder A* - Berechnung durchaus brauchbar.
Dijkstra und die kurzen Wege
[siehe hierzu auch: E.W. Dijkstra „A Note on Two Problems in Connecting with Graphs“, Numerische Mathematik, Vol. 1, Springer-Verlag, Berlin, 1959]
Bereits in den 50er Jahren befasste sich Dijkstra intensiv mit der Suche nach dem kürzesten Pfad.
Er geht dabei von einem zusammenhängenden Graphen aus und ermittelt anhand der Kantenlängen den kürzesten Pfad von einem Startknoten zu einem Zielknoten. Dabei wird mit verschiedenen Listen gearbeitet, in welche noch zu untersuchende und bereits untersuchte Knoten eingefügt werden. Untersucht werden immer die Nachbarn des Knoten, der bisher die geringste Entfernung zum Startpunkt hat. In einer weiteren Liste wird dabei der Vorgänger des zu untersuchenden Knotens gespeichert. So kann man am Ende des Algorithmus ausgehend vom Zielknoten den Weg rückwärts zeichnen.
Erläuterungen des Dijkstra-Algorithmus findet man unter
http://www.irf.de/seminar/schlette/stdt_1.htm
http://www-lehre.inf.uos.de/~graph/skript/6_1_Algorithmus_von.html
http://www.in.tum.de/~muellemi/amr/report/node16.html
Applets zum Thema:
http://www.stud.fernuni-hagen.de/q4119142/dijkstra.html
http://www.unet.univie.ac.at/~a9825992/Java/Dijkstra.html
I see A Star
"Wir sind dem Stern gefolgt." - "Sternhagelvoll seid Ihr!" (Life of Brian)
A* (lies: A Star) ist ebenso wie Dijkstra ein Algorithmus zur Suche eines kürzesten Pfades in einem zusammenhängenden Graphen. Allerdings wird die Datenstruktur hier um eine Schätzung der Entfernung des jeweiligen zu untersuchenden Knotens zum Zielknoten ergänzt. Sofern diese Schätzung exakt ist, ergibt sich somit der Gesamtweg als Summe der Entfernung vom Startpunkt zu einem beliebigen Punkt X und der Entfernung von eben diesem Punkt X zum Zielpunkt. Auch dieser Algorithmus arbeitet mit unterschiedlichen Listen für bereits untersuchte und noch zu untersuchende Punkte, wobei immer der Knotenpunkt aus der Liste der noch zu untersuchenden Punkte ausgewählt wird, dessen Summe aus bisherigem Weg vom Start und geschätztem Weg zum Ziel minimal ist. Dies ist auch der wesentliche Unterschied zum (langsameren) Dijkstra-Algorithmus, der immer den Knoten mit der geringsten Entfernung zum Startpunkt expandiert.
Erläuterungen des A*-Algorithmus findet man unter:
http://www.irf.de/seminar/schlette/stdt_0.htm
http://www.in.tum.de/~muellemi/amr/report/node17.html
Schlank ist schick
"Dick? Wer ist hier dick?" (Obelix)
So schnell die aktuellen CPUs und Grafikkarten heute auch sind (ja, ja, ich weiß, in zwei Jahren lachen wir alle herzhaft über die alten lahmen Kisten), die Algorithmen sind immer noch relativ langsam. Je nach Größe der Weltkarte kann eine Wegberechnung schon mal zwischen 1 Sekunde und 1 Minute dauern, gerade dann natürlich wenn mehrere Einheiten vom Spieler oder auch vom Computer auf Reisen geschickt werden. Wie können wir den jeweiligen Algorithmus also optimieren?
1. Möglichkeit: Schränken Sie die Anzahl der zu untersuchenden Felder ein. In der Regel befinden sich Start und Ziel nicht an entgegengesetzten Enden der Weltkarte, so dass nicht alle Felder der Welt untersucht werden müssen. Benutzen Sie Start und Ziel als Eckpunkte des Suchfeldes. Allerdings sollten Sie die Feldgrenzen auf Hindernisse untersuchen und gegebenenfalls das Feld vergrößern, um einen Weg um dieses Hindernisse herum zu finden.
2. Möglichkeit: Benutzen Sie für einfache Teilstücke einfache Algorithmen. Wenn Ihre Spielfigur über eine größere Strecke einfach geradeaus rennen kann, lassen Sie sie doch mit Hilfe eines Linienalgorithmus laufen. Dies geschieht solange bis sie auf ein Hindernis stößt, dann kann man mittels Dijkstra- oder A*-Algorithmus einen Weg um dieses Hindernis ermitteln.
The next Generation???
"... to boldly go where no one has gone before" (Star Trek - The next Generation)
Die bisher aufgezeigten Algorithmen gehen von einer bekannten statischen Umwelt aus. Auf Fehler oder dynamische Veränderungen können sie nur schwer, nämlich durch Neuberechnung der Wege reagieren.
1994 hat Anthony Stentz einen Algorithmus zur Wegfindung in einer dynamischen Umgebung veröffentlicht: D* (Dynamic A*). Der Kniff dabei ist, dass die Spielfigur eine individuelle, eventuell fehlerhafte Weltkarte besitzt. Anhand dieser Karte wird zu Beginn der optimale Weg berechnet. Die Figur folgt dem berechneten Pfad, bis sie am Ziel ankommt oder auf einen Fehler stößt. Ein Fehler kann in diesem Zusammenhang ein Hindernis an einer unerwarteten Stelle, das Fehlen eines Hindernisses an einer erwarteten Stelle oder das Auftauchen eines Gegner (was ja eigentlich auch nur eine andere Art von Hindernis ist) sein. Wird so ein Fehler ermittelt, wird der Weg an dieser Stelle neu berechnet, um das Hindernis zu umgehen.
Ausführlichere Darstellungen des D*-Algorithmus findet man unter:
http://www.frc.ri.cmu.edu/~axs//
http://www.kbs.uni-hannover.de/Lehre/KI1/Presentationen/presentation9798/esprit/Dhyper.htm
Zum Beispielprogramm
"And now: Something completely different!" (Monty Python)
Das beiliegende C++-Beispielprogramm präsentiert mit Ausnahme von D* die hier vorgestellten Wegfindungs-Algorithmen. In einer 40x40 Felder großen Weltkarte können Hindernisse gesetzt werden, durch Anklicken eines Feldes mit der linken Maustaste kann dieses Weltfeld auf ein höheres Niveau gebracht werden, mit der rechten Maustaste wird das Feld abgesenkt. Nach Setzen von Start und Zielpunkt, kann aus dem Menü ein Algorithmus ausgewählt werden. Der Weg wird dann berechnet und blau dargestellt.
Die Darstellung muss manuell über das Datei-Menü gelöscht werden, da sonst Wege auch als Hindernisse interpretiert werden. (Sorry, ist halt nur 'ne simple Demo!)
Lob und Schelte werden gerne entgegengenommen unter: