


|

|
Als ich mich ransetzte, um diese Einführung zu schreiben, da trieb mich nicht so sehr die Freude, zu zeigen, was es für komplizierte Programmiertechniken gibt. Vielmehr will ich zeigen, wie man mit Hilfe von Programmierung "denken" kann, Probleme analysieren und lösen und vielleicht auch mit ihnen spielen kann. Was man mit Programmierung machen kann, ist mir wichtig, nicht die Tätigkeit selbst.
Deshalb will ich hier in diesem Kapitel mal eine etwas ungewöhnliche Überlegung und ihre Bearbeitung einschieben. Ich nehme an, viele von Ihnen kennen/kannten die Show "Wer wird Millionär?" von Günter Jauch. Ein Trivial Pursuit für's Fernsehen. Ein Kandidat beantwortet Fragen von Jauch, indem er aus vier Antworten auswählt. Wählt er falsch, hat er verloren. Wählt er richtig, kommt die nächste Frage und sein möglicher Gewinn verdoppelt sich. Wenn er falsch rät, darf er den schon erreichten Gewinn mit nach Hause nehmen. Bei 50 Euro fängt's an und geht bis 1 Million Euro.
Es gibt während dem Spiel drei Joker. Einmal darf der Kandidat das Publikum befragen, einmal darf er sich 2 von 4 Antwortalternativen streichen lassen und einmal darf er jemand zuhause anrufen, den er kennt.
Wenn Sie die Show kennen und schon selbst angesehen haben, dann werden Sie sich sicher auch schon vorgestellt haben, dass Sie selbst im Kandidatenstuhl sitzen. Und jeder wird sich so seine Strategie zurechtgelegt haben, wie er mit den Jokern umgeht. Der eine sagt: "Sobald ich auch nur ein bisschen unsicher bin, verwende ich einen Joker. Schliesslich geht es von Anfang an umd nicht wenig Geld und vor allem: Wenn ich raus bin, nutzen mir die übrigen Joker eh nichts mehr." Der andere sagt: "Ne, Blödsinn. Am Anfang sind die einfachen Fragen. Wenn ich da schon die Joker einsetze, bin ich bei den schwierigen Fragen verloren und erreiche nie die Million. Ich muss am Anfang eine kleine Unsicherheit riskieren, damit ich später überhaupt eine Chance habe, die die schwiergen Fragen zu beantworten!"
Was ist richtig davon? Sie meinen, dass man das nicht objektiv beantworten könnte? Na, schauen wir mal, was mit dem C16 und ein bisschen Nachdenken denn so geht.
Was uns interessiert, sind zwei Fragen:
Bei jeder Frage gibt es eine Wahrscheinlichkeit, dass der Kandidat die Frage richtig beantwortet. Die gross die Wahrscheinlichkeit bei jeder Frage sein soll, können wir in die folgende Tabelle eintragen.
| Frage | Gewinn | Wahrscheinlichkeit |
| 1 | 50 | 100 |
| 2 | 100 | 95 |
| 3 | 200 | 90 |
| 4 | 500 | 90 |
| 5 | 1000 | 85 |
| 6 | 2000 | 85 |
| 7 | 4000 | 80 |
| 8 | 8000 | 70 |
| 9 | 16000 | 60 |
| 10 | 32000 | 50 |
| 11 | 64000 | 40 |
| 12 | 125000 | 30 |
| 13 | 250000 | 25 |
| 14 | 500000 | 25 |
| 15 | 1000000 | 25 |
Ein Joker soll die Wahrscheinlichkeit (einfachheitshalber) auf 100% setzen.
Nun muss der Computer ran. Es soll einfach spielen. Eine Frage besteht darin, dass gemäss der Wahrscheinlichkeit der Fragennummer gewürfelt wird. Erinnern Sie sich an die RND()-Funktion! Und zwar nur zwischen 0 und 1. Kommt 0 heraus, ist das Spiel vorbei und der bisher erreichte Gewinn wird notiert. Kommt 1 heraus, kommt die nächste Frage.
Am Anfang jeder Runde werden drei Fragen (durch den Benutzer/zufällig/systematisch in einer Schleife: Wie Sie wollen) ausgewählt, bei denen der Joker eingesetzt wird. Z.B. Frage 2,5 und 7. Bei diesen wird die Wahrscheinlichkeit auf 100% gesetzt, d.h. die Frage wird sicher beantwortet (Sie müssen in diesem Fall die RND()-Funktion gar nicht mehr bemühen.)
Sie sollten jede Jokersetzung, also jedes Jokerfragentripel, nicht nur einmal durchspielen, sondern mindestens 20mal, besser 100mal oder mehr. Denn das Ergebnis hängt ja auch vom Zufall ab. Wenn man aber oft spielt, dann hängt der Anteil, mit dem die Million erreicht wird und der mittlere Gewinn in den Spielen nicht mehr so vom Zufall ab.
Wir haben noch ein kleines Problem: Wie bekommen wir die Tabellenwerte ins Programm? Nun, mit Arrays ist das an sich kein Problem, aber nun 30 Zeilen mit LET X(0,0)=50, LET X(0,1)=100, LET X(1,0)=100,... zu schreiben, ist auch irgendwie blöd. Es gibt eine kleine Vereinfachung, den DATA/READ-Befehl.
Dazu schreibt man in eine Zeile hinter den DATA-Befehl (am besten ganz ans Programmende) die Zahlenwerte in der Reihenfolge, in der sie nachher in das Array geschrieben werden sollen. So kann man viele Zahlen sozusagen mitten in den Programmtext schreiben:
10 DIM X(I) 15 RESTORE 50 20 FOR I=0 TO 9 30 READ X(I) 40 NEXT I 50 DATA -19,31.5,22.3,34,-4.5,9.3,-298,877,-29,76.39
Im Beispielprogrämmchen stehen die Zahlen in der DATA-Zeile 50. Wir sehen auch schon, wie wir dann an diese Zahlen rankommen. Zunächst teilen wir dem Computer mit, wo die Zahlen stehen, die er abholen soll: RESTORE 50. Das heisst: "Hole sie in Zeile 50". Da steht unser DATA-Befehl mit Zahlenliste. Mit jedem READ
So. Jetzt sind Sie dran! Machen Sie sich an Ihre Übungsaufgabe! Schreiben Sie ein Programm, dass Ihnen den mittleren Gewinn und die Milliongewinnwahrscheinlichkeit für eine bestimmte Jokersetzung ausgibt! Und stellen Sie damit fest, welche Jokerstrategie am effektivsten ist!
Zugegeben: Obwohl das eigentliche Programm nicht kompliziert ist, wird es nicht einfach sein, zu verstehen, was der Knilch in diesem Kapitel eigentlich meint. Wie dieses "Frage und Antwort"-Geschehen in ein Programm umgemünzt werden soll. Und wie da auch noch der Joker irgendwo auftauchen soll. Deshalb hier noch ein paar Hilfestellungen, u.a. der Programmteil, der das eigentliche Spiel darstellt. Wenn Sie dann immer noch nicht zurechtkommen - keine Panik, schauen Sie sich einfach im nächsten Kapitel die fertige Lösung an. Sie sind auch schon sehr gut, wenn Sie die nachvollziehen und verstehen können!
Also: Was passiert, wenn Günter Jauch einem Kandidaten in der Sendung eine Frage stellt? Der Kandidat wählt aus vier Antworten eine aus. Tut dabei sein Bestes, die richtige Antwort zu finden. Klappt natürlich nicht immer. Manchmal wählen die Kandidaten ihre Antwort sogar auf gut Glück. Wenn der Kandidat nicht viel Ahnung hat, dann wählt er sogar immer auf gut Glück, weil er ja nichts weiss, was ihn der richtigen Antwort näher bringen würde als allen anderen. Das Ganze ist also eine Art Lotteriespiel. Wenn der Kandidat eine gute (Jauch-)Bildung hat, dann ist die Wahrscheinlichkeit, dass er die richtige Antwort zieht, mehr als ein Viertel, mehr als 25%. Wenn er es "hundertprozentig sicher" weiss (und damit recht hat), ist sie sogar 100%. Das heisst, wir können jedes Spiel darstellen als eine Lottoziehung mit dem Ausgang "Richtig" und "Falsch" und einer Wahrscheinlichkeit p für "Richtig", die zwischen 25% und 100% schwankt - je nachdem, wie gut der Kandidat ist.
So, nun sind wir der Sache schon näher. Wenn nun ein Joker ins Spiel kommt, gehen wir davon aus, dass der Kandidat nach Anwendung des Jokers die Antwort sicher weiss: p geht auf 100%. (Das stimmt nicht ganz. Aber für unsere vereinfachte Betrachtung hier reicht diese Annahme vollkommen aus.)
Wie sieht nun eine Frage aus? Wir nehmen eine Wahrscheinlichkeit p. p nehmen wir aus der Tabelle von oben. Wenn der Kandidat einen Joker anwendet, ist die Frage gelaufen und das Ergebnis der Frage ist "Richtig". Wenn nicht, dann lassen wir den Computer würfeln. Zunächst eine gleichverteilte Zufallszahl zwischen null und eins: LET X=RND(1). Wenn X dann kleiner ist als p, dann ist die Antwort "Richtig". Ansonsten "Falsch".
Ein ganzes Spiel besteht darin, von Frage 1 ab Fragen zu spielen. Jedesmal mit dem p, das in der obigen Tabelle der entsprechenden Frage zugeordnet sind. Da die Fragen immer schwieriger werden, wird das p immer kleiner. Es kann aber natürlich nicht unter 25% sinken. Wenn eine Antwort "Falsch" lautet, ist das Spiel aus. Ergebnis ist der bisher erreichte Gewinn. Wenn alle Fragen "Richtig" ergeben, ist der letzte Gewinn eine Million.
Ziel ist es nun, den Computern viele solche Spiele spielen zu lassen und den mittleren Gewinn zu ermitteln und die Zahl der Spiele zu zählen, die 1 Million ergeben haben.
Jetzt klarer? Wenn immer noch nicht, dann schauen Sie sich einfach die Zeilen 2000 bis 2300 im Listing des folgenden Kapitels an. In 2200 bis 2260 wird eine Frage durchgespielt, in 2000 bis 2150 ein Spiel.
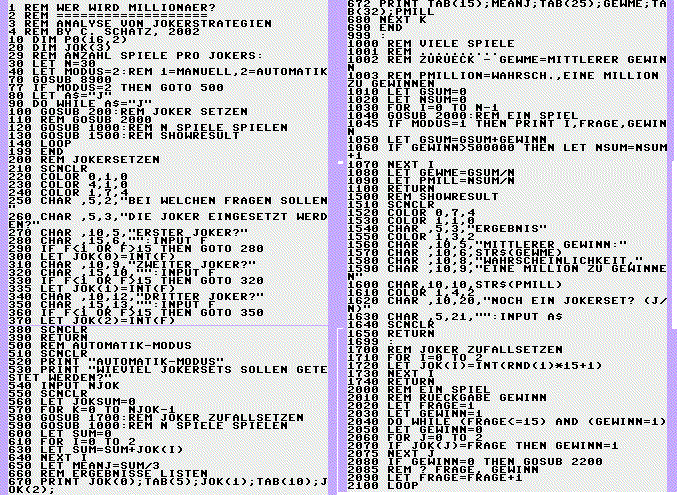
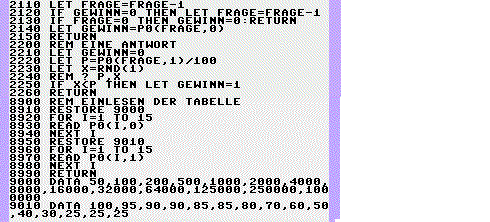
Aufbau des Programms:
| 2200 bis 2300 | Durchführung einer Antwort (Frage) |
| 2000 bis 2200 | Ein Spiel |
| 1000 bis 1500 | Viele Spiele |
| 200 bis 400 | Benutzerdialog: Joker setzen |
| 1500 bis 1650 | Benutzerdialog: Ergebnisse anzeigen |
| 500 bis 1000 | Spezialmodus |
| 0 bis 50 | Deklarationen und Setzen der Systemgrössen |
| 50 bis 200 | Hauptprogramm |
Im Hauptprogramm wird zunächst die Modus-Variable abgefragt, und es wird ggf. in einen speziellen Programmmodus gesprungen. Ansonsten wird eine Schleife betreten, die der Benutzer am Ende der Programmbenutzung mit "N" wieder verlassen kann. Nun werden um Unterprogramm "Joker setzen" die Joker vom Benutzer auf die Fragen gesetzt, in denen sie angewandt werden sollen. Anschliessend "N Spiele spielen" aufgerufen. Das wiederum ruft N-mal "Spiel spielen" auf. Soweit der grobe Aufbau.
Der Spezialmodus wird bei den Ergebnissen im nächsten Abschnitt erläutert.
Haben Sie ein paar Jokersetzungen ausprobiert? Sie werden feststellen, dass der Rechner für jedes Spiel ca. eine halbe Sekunde braucht (etwas schneller als in der echten Show also...). Wenn wir zur Sicherheit 1000 Spiele spielen lassen (N=1000), um einen genauen Mittelwert für Gewinn und Millionenwahrscheinlichkeit zu ermitteln, sind das 500 Sekunden, als ca. 8 Minuten pro Jokersetzung. Es gibt bei 3 Jokern und 15 Fragen eine Menge verschiedene Setzungen (dreitausend und noch was). Die können wir so also nicht alle durchprobieren.
Nun, man kann N auch kleiner wählen. N=100 z.B. oder N=30 oder N=10. Wieviel man mindestens braucht, können Sie dadurch testen, dass Sie diesselben N Spiele zweimal hintereinander durchspielen lassen und die Mittelwerte vergleichen. Weichen Sie zu stark voneinander ab, haben Sie N zu klein gewählt. Ich habe auf diese Weise herausgefunden, dass N=100 schon sein sollte.
Ich bin dann auf die Idee gekommen, den Computer die Joker einfach zufällig wählen zu lassen. Das ist der Spezialmodus. Sie brauchen sich das aber nicht weiters anzuschauen - das funktioniert nicht. Man kann am Ergebnis nichts erkennen, die Mittelwerte scheinen ziemlich willkürlich hin und her zu schwanken.
Danach bin ich auf den Gedanken gekommen, im manuellen Modus die Joker einfach im Block zu setzen, zuerst ganz am Anfang und dann immer weiter nach oben zur Frage 15 zu schieben. Das ergab etwas Sinnvolles für die Gewinne. Die Millionenwahrscheinlichkeiten waren immer null - die Million ist schon sehr unwahrscheinlich. Wir müssten sehr, sehr viele Spiele spielen, um diese Unwahrscheinlichkeiten so genau bestimmen zu können, damit man sie vergleichen kann. Daher habe ich Zeile 1060 geändert. Ich habe den Computer zählen lassen, wenn ein Gewinn grösser als 32000 ist. Da sind die Wahrscheinlichkeiten grösser. Schliesslich hat mich interessiert, was passiert, wenn man einen Joker aus dem Block rausnimmt. Daher habe ich dann noch Kombinationen wie "1 Joker am Anfang, 2 in der Mitte" oder "2 am Anfang, einer in der Mitte" getestet. Das Ergebnis sehen Sie unten.
| Joker1 | Joker2 | Joker3 | Gewinn | p |
| 1 | 2 | 3 | 4648 | 0.02 |
| 4 | 5 | 6 | 7653 | 0.01 |
| 7 | 8 | 9 | 11016 | 0.05 |
| 10 | 11 | 12 | 10433 | 0.06 |
| 13 | 14 | 15 | 4543 | 0 |
| 3 | 8 | 9 | 10206 | 0.04 |
| 3 | 4 | 9 | 5981 | 0 |
Das Ergebnis ist eindeutig: Am Besten für Gewinn und 64000-Wahrscheinlichkeit ist es, wenn die Joker in der Mitte benutzt werden, zwischen Frage 7 und 12. Die vorgezogene oder nachgelagerte Benutzung eines Jokers bringt nichts.
Man sieht also, dass wir mit unserem kleinen Programm eine nette Frage beantworten konnten, bei der uns anfangs gar nicht eingefallen wäre, dass man sie überhaupt so klar beantworten kann.
Im Beispielprogramm kommen ein paar Kommentarzeilen vor, z.B. Zeile 110, die eigentlich gar keine Kommentarzeilen sind, sondern Befehlszeilen mit einem REM davor. Hier sind ehemalige Befehlszeilen durch Einfügen eines REM's deaktiviert worden. Man kann sie bei Bedarf so wieder schnell aktivieren und Sie können anhand dieser Zeilen sehen, wie die Programmentwicklung ursprünglich lief.
Ich habe zuerst die DATA-Zeilen und die Einleseroutine 8900 bis 9100 geschrieben und getestet. Dann bin ich vom Kern zur Schale vorgegangen, habe also zuerst mit der kleinsten Einheit, der einzelnen Frage in Zeile 2200 angefangen. Man sieht das noch an dem auskommentierten PRINT-Befehl in Zeile 2240. Hier habe ich mir zunächst beim Testen der Routine für jede einzelne Frage p und x, Wahrscheinlichkeit und Würfelergebnis ausgeben lassen. Als das funktionierte, konnte ich die Zeile auskommentieren.
Als Nächstes habe ich die Routine für ein Spiel aufgesetzt. In Zeile 2085 habe ich mir die das Ergebnis jeder Frage ausgeben lassen, um zu kontrollieren, wie das einzelne Spiel verläuft, welche Fragen "der Kandidat" noch richtig beantwortet. So konnte ich beurteilen, ob die letzte erreichte Frage auch richtig ermittelt wird.
Als auch die Spielroutine richtig funktionierte, ging's zum "Turnier", zu der Routine, die N Spiele durchspielt. Hier wird ohnehin in Zeile 1045 das Ergebnis jedes Spiels ausgegeben.
Was lernen wir also draus? Man muss ein Programm nicht von vorne nach hinten schreiben, sondern kann es ein bisschen chaotisch angehen: Man löst zuerst die Teilaufgäbchen, die einem leicht und beherrschbar erscheinen, in kleinen Routinen. Dann bastelt man diese Routinen zu anderen Routinen zusammen, die schon grössere Aufgaben lösen. Und so weiter. Beim Test der Routinen sollte man mit PRINT-Anweisungen (und ggf. auch Input's dahinter, um die Ausgabe auch lesen zu können), nicht sparen. Und man sollte die PRINT's nicht einfach löschen, wenn man sie nicht mehr braucht, sondern auskommentieren. Es kann ja sein, dass man sie später testweise nochmal braucht.