Was ist ein Computer? Sie meinen, das sei schwer zu beantworten? Überhaupt nicht. "To compute" kommt aus dem Englischen und heisst "Rechnen". Genauer gesagt: "Rechnungen durchführen", die Tätigkeit des Rechnens also. Ein Computer ist ein Rechner. Um mit Zahlen zu rechnen.

Das sieht man ihm heute zugegebenermassen nicht mehr so an. Man muss schon ganz schön herumsuchen, bis man auf einem heutigen PC irgendwo etwas findet, mit dem man rechnen kann. Alles mögliche kann man: Surfen, Zeichnen, Malen, Texte schreiben, Musik hören. Aber rechnen?

Nun, man kann es so betrachten: Bei all diesen Tätigkeiten - Surfen, Zeichnen usw. - wird der Computer sozusagen "missbraucht". Was er im Inneren macht, wenn wir Texte schreiben, ist, in einer gewissen Form zu rechnen.

Bei den kleinen Computern wie dem C16 merkte man das schon eher. Die waren zu klein, um so ohne Weiteres andere Dinge wie Textverarbeitung oder Musik "rechnen" zu können. Man war mit dem technischen Gerät als solches stärker konfrontiert, als heute, wenn man es anschaltete. Das haben Sie gerade gesehen.

Da ein Computer ein Rechner ist, müsste der Taschenrechner ein Taschencomputer sein. Ist das so? Nein. Das heisst, nicht unbedingt. Denn in den letzten fünfzig Jahren (so lange existieren Computer ungefähr), hat man sich darauf geeinigt, nur die Rechner "Computer" zu nennen, die "programmierbar" sind. Ein Computer ist also ein programmierbarer Rechner. Und das war's auch schon. Was "programmierbar" heisst, werden wir noch sehen.

Manuelles Rechnen

Unser Leben hat viel mit Rechnen zu tun. In der Schule müssen Aufgaben in Mathe und Physik gelöst werden, im Haushalt müssen die Ausgaben ausgerechnet werden, mit Mieten und Aktien und Wohnungskauf muss rechnerisch umgegangen werden, in der Arbeit müssen Statistiken ausgerechnet und Rechnungen bearbeitet werden usw. An Anwendungen für unseren kleinen C16 sollte es also nicht fehlen.

Wir wollen uns aber eine andere Aufgabe stellen. Eine der berühmtesten Aufgaben der Mathematik. Wir wollen Primzahlen ausrechnen.

Was ist eine Primzahl? Das ist eine Zahl, die nur durch sich selbst und durch Eins ohne Rest teilbar ist. Und die Frage ist: Wieviel solche Primzahlen gibt es eigentlich?

Schauen wir uns mal die ersten Primzahlen an. 1 ist eine Primzahl. Denn 1 ist nur durch sich selbst (1) und durch 1 teilbar. 2 ist auch eine Primzahl. 3 auch: 3 ist durch 1 und durch 3 teilbar. 4 ist keine Primzahl. 4/2=2. Das heisst, 4 ist ausser durch 4 und durch 1 auch durch 2 ohne Rest teilbar. 5 ist wieder eine Primzahl. 6 nicht. Keine gerade Zahl kann eine Primzahl sein, denn sie ist natürlich immer durch 2 teilbar. 7 ist wieder ein Primzahl. 9 ist keine Primzahl, denn sie ist auch durch 3 teilbar. 11 ist dafür wieder eine Primzahl.

Die ersten Primzahlen sind also:

1, 2, 3, 5, 7, 11

Fast jede ungerade Zahl. Aber eben nicht jede. Bei weitem nicht jede. Schauen wir uns 47 bis 53 an. Von 47 bis 53 sind nur 47 und 53 Primzahlen. Und 55 und 57 dann schon wieder nicht.

Gibt es eine Formel, die uns sagt, welche Zahl eine Primzahl und welche nicht? Das wissen wir nicht. Aber die Mathematik hat in ihrer viertausendjährigen Geschichte bisher keine gefunden. So gibt es nur einen Weg, herauszufinden, ob z.B. 221 eine Primzahl ist: Wir müssen es ausprobieren. Alle möglichen Teiler durchprobieren. Machen Sie das mal mit dem C16! Das ist eine gute Übung, um mit ihm warmzuwerden! Es ist nicht soviel Arbeit, wie es auf den ersten Blick aussieht.

Ob 221 eine Primzahl ist oder nicht, verrate ich erst am Schluss dieses Kapitels. Aber wenn Sie hier engagiert gerechnet haben, werden Sie gemerkt haben, dass Sie eine Zahl immer wieder eintippen müssen: 221. Ein bisschen blöd. Man sollte dem Rechner sagen können: "Merk dir mal die 221". Der C16 müsste dafür ein Gedächtnis haben, einen elektronischen Speicher. Manche Taschenrechner haben ja so etwas, eine Speichertaste. Hat der C16 auch so eine?

Hat er. Dazu brauchen wir neben dem '?' aber nun ein weiteres Wort, das er versteht. Dieses Wort ist LET. Mit LET kann man eine Zahl speichern:

LET A=221
READY

Das =-Zeichen finden Sie auf der Akzent-Taste links neben BACKSPACE. Und: ENTER-Taste nicht vergessen!

Der Name des Speichers ist A. Man nennt das auch eine Variable. Aber was nun? Nichts wird angezeigt! Nein. Ist ja auch klar. Wir haben ja auch nichts gerechnet. Nur abgespeichert.

Schauen wir aber nun, ob sich der C16 die Zahl auch behalten hat. Tippen wir ein:

? A
221

READY

Tatsächlich! Hat er! Und "A" geht schneller als "221"! Nun können wir also viel leichter tippen:

? A/3
73.6666667

READY
? A/5
44.2

READY

Nun wissen wir auch, warum der C16, anders als ein Taschenrechner, auch Buchstabentasten braucht. Wegen der Speicher.

Hat der C16 nur einen Speicher? Wir können ja versuchen, auch mal in B was abzuspeichern:

LET B=11

READY
? B
11

READY

Prima. Klappt offenbar. Es ist sogar so, dass man den Speichern nicht die Buchstaben des Alphabets nach zuweisen muss, sondern ihnen eigene Namen nach Gutdünken geben kann. Z.B. kann

LET PI=3.14159

Rechnungen speichern

In der Schule und später im Studium oder in technischen Berufen hat man es immer wieder mit Formeln zu tun. Formeln sind mathematische "Kochrezepte". Sie enthalten Buchstaben, für die wir bekannte Zahlen einsetzen und sie liefern uns dann die gesuchte Zahl. Wie lang ist die Grundseite eines rechtwinkligen Dreiecks? c=sqr(a^2+b^2), a und b sind die Längen der Schenkel. Das "^" steht für "hoch". Im C16 wird dafür allerdings ein Pfeil nach oben verwendet, der über der Null steht. Also: Shift und Null gleichzeitig liefert den Pfeil, der auf dem C16 "hoch" bezeichnet. Und wir schreiben hier für diesen Pfeil "^". Es gibt noch andere Formeln: Wie schnell fährt ein Auto (gemessen in km/h), das 320 m in 5 s zurückgelegt hat? v = s / t * 3.6, s=320m, t=5s.

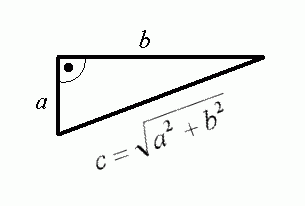
Nehmen wir an, wir wollen eine Tabelle erstellen, die zu jeder Länge von a und b die Länge von c angibt, der Grundseite des Dreiecks:

        a                      b        c
        10cm                10cm        ?
        20cm                10cm        ?
        30cm                10cm        ?
        40cm                10cm        ?
        50cm                10cm        ?
        10cm                20cm        ?
        20cm                20cm        ?
        30cm                20cm        ?
        40cm                20cm        ?
        50cm                20cm        ?
        10cm                30cm        ?
        20cm                30cm        ?
        30cm                30cm        ?
        40cm                30cm        ?
        50cm                30cm        ?
        10cm                40cm        ?
        20cm                40cm        ?
        30cm                40cm        ?
        40cm                40cm        ?
        50cm                40cm        ?
usw.

Das gibt eine nette Rechnerei, selbst, wenn wir auf die Idee kommen, den Wert von b jeweils abzuspeichern:

LET B=10

READY
? SQR(10^2+B^2)
14.142136

READY
? SQR(20^2+B^2)
22.36067

READY
? SQR(30^2+B^2)
31.6227766

READY
...
...
...

Das ist schon ein nerviges Getippe! (Vor allem, weil wir jetzt am Anfang noch nicht genau wissen, wo die ganzen Sonderzeichen sind. Das Plus ist auf der ß-Taste und das Fragezeichen über dem Bindestrich...) Achtung! Da kann's dann auch noch einen ganz üblen Vertipper geben: Wenn man Shift+ß eingibt, erscheint ebenfalls ein Plus. Es ist allerdings ein bisschen grösser und es "funktioniert" in der Formel nicht wie ein Plus. Der C16 meldet dann "Syntax Error". Und man sieht's einfach nicht, da ja das Plus eigentlich genau da steht wo es stehen soll - es ist nur das falsche.

Bald wünschen wir uns, dass wir diese elende Formel selbst irgendwie abspeichern könnten und nicht dauern immer wieder das "SQR(" und dann "^2" usw. eintippen müssten. Abgesehen davon, dass man sich doch dabei sehr leicht vertippen kann.

Wir tippen die Formel ein, unter Benutzung von A und B. Aber halt - vor das "?" schreiben wir eine Zahl, und zwar eine Eins:

1 ? SQR(A^2+B^2)

Achten Sie darauf, zwischen dem 1, ? und dem SQR jeweils ein Leerzeichen zu schreiben.

Die 1 ist also neu. Was ist passiert? Gar nichts, wie es scheint. Weniger als nichts. Der Computer hat kein Ergebnis ausgespuckt. Er hat nicht mal "READY" geschrieben. So was. Was soll denn das?

Nun: Der Computer hat die Zeile nur gespeichert. Und zwar im Speicher Nummer Eins. Das bedeutet die Eins vor der Anweisung. Er hat nicht nur eine Zahl, er hat die ganze Rechnung gespeichert. Wenn wir den Befehl LIST eingeben, dann können wir uns den Inhalt dieses Rechnungsspeichers wieder ansehen:

LIST

1 PRINT SQR(A^2+B^2)

READY

Schon wieder eine Überraschung. Da ist was anders. Wenn wir das, was hinter der 1 kommt, mit dem vergleichen, was wir eben oben eingetippt haben, dann ist das "?" durch ein ganzes Wort ausgetauscht. PRINT steht jetzt da. Das liegt daran, dass das "?" nur eine Abkürzung ist, für einen sehr oft gebrauchten Befehl (wir haben ihn ja schon oft gebraucht!), den PRINT-Befehl. Der eben sagt: "Drucke die folgende Rechnung auf dem Bildschirm aus!".

LIST bedeutet also, dass wir uns alle gespeicherten Rechnungen ausgeben lassen. Geben wir mal noch eine zweite Rechnung ein. Und zwar hinter eine "Zwei". Wir sagen: Wir speichern die Rechnung in "Zeile 2".

2 ? SQR((A+10)^2+B^2)

Wir erhöhen also A um 10 und rechnen dann wieder die Formel aus. Das ist die zweite Zeile. Und dann geben wir LIST ein. Jetzt sehen wir:

LIST

1 PRINT SQR(A^2+B^2)
2 PRINT SQR((A+10)^2+B^2)

READY

Aha. Jetzt sind schon zwei Rechnungen hintereinander gespeichert. Eine in Zeile 1, die andere in Zeile 2. Und was machen wir jetzt damit? Wir wollen die Rechungen ausführen! Die Zahlen in A und B sind ja schon gespeichert. Wir geben nun den Befehl GOTO ein. Mit GOTO führt man die gespeicherten Rechnungen hintereinander aus. Wobei man hinter GOTO die erste auszuführende Rechnung angibt (deren Zeile), d.h hier die 1

GOTO 1

0
10

"GOTO 1" hiess: Führe nun diese beiden Rechnungen aus. Zuerst die hinter der "1" und dann die hinter der "2". Aber es kommt nicht das heraus, was wir eigentlich wollten. "Null" macht keinen Sinn. Aber seien wir mal ehrlich: Das kann ja auch gar nicht sein. Wir haben ja in A und B noch gar nichts abgespeichert. Denn, man merke sich: Sobald wir Rechnungen abspeichern, gehen die Zahlenspeicher verloren. Das mag dumm sein, aber das ist nun mal so. Also, wir speichern also auch in A und B eine Zahl.

LET A=10

READY
LET B=10

READY

LIST

1 PRINT SQR(A^2+B^2)
2 PRINT SQR((A+10)^2+B^2)

READY

LIST

1 PRINT SQR(A^2+B^2)
2 PRINT SQR((A+1X)^2+B^2)

READY

? A
0

READY
? B
0

READY